Трехходовые регулирующие вентили в настоящее время с успехом используются в решении регулирующих узлов, благодаря их способности смешивать (или распределять) теплоноситель в требующемся соотношении для достижения необходимой температуры. Обычно трехходовая арматура на входах обозначается буквами, вход примарной (первичной)воды обозначается буквой А, труба короткого соединения (обратная ветвь) буквой В, и общий выход (постоянно открытый) АВ.
Для беспроблемной функции смешивания следует следить за тем, чтобы А и В не были загружены различным дифференциальным давлением (перепадом давления). В противном случае могут возникнуть проблемы с возможным поворотом течения во входе В а определенных рабочих условиях, что может вызвать частичную или полную потерю смесительной функции.
Трехходовые регулирующие вентили могут использоваться в качестве смесителя или распределителя, если позволяет конструкция, о чем должна свидетельствовать проектная документация производителя.
Расчет трехходового регулирующего вентиля отличается своей спецификой, особенно там, где технологическое включение предполагает нагрузку вода А дифференциальным давлением.
В следующей части мы предлагаем Вашему вниманию способ проектирования и расчета трехходового регулирующего вентиля согласно рис. 2.10., которые часто применяется в связи с простой (кажущейся) в зависимых по давлению присоединениях.
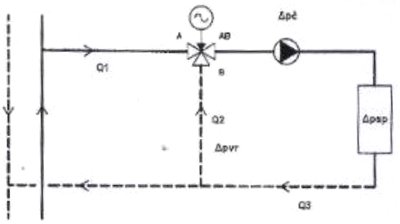
Рис. 2.10. Трехходовой смесительный вентиль, наружный дифференц. давлением.
Для определения проведения трехходового регулирующего вентиля его можно заменить двумя регулирующими вентилями, которые имеют одинаковые Kvs, избирательную характеристику ветвей А и В, а для их общей зависимости хода действительно: hА=1 - hВ1 (см. рис. 2.11).
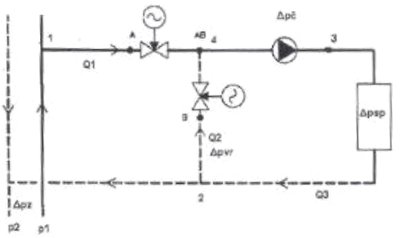
Рис. 2.11. Замена трехходового смесительного вентиля двумя двухходовыми вентилями.
Для удобства осуществим выведение по упрощенным формулам для вычисления Kv, действительным для воды, следовательно предположим, что константная плотность воды ρ=1000 kg.m-3, предположим развернутый турбулентный паток и возможность возникновения кавитации.
Для указанной схемы действительно следующее:
-система нагружена перепадом давления между подачей и обратным трубопроводом ∆ρz
- давление насоса ∆ρč не зависит от циркуляционного количества (подачи)
-пренебрегаем сопротивлениями подающей части трубопровода между точкой 2 и присоединением обратного трубопровода
-определим размеры вентиля для номинального расхода Q3nom , который должен протекать через систему при полностью закрытой ветви А и полностью открытой ветви В. При таком номинальном расходе потеря давления потребителя, включая трубопровод от точки 4 до точки 2, равна ∆ρsp , потеря давления обратной ветви от точки 2 до точки 4, не считая потери на вентиле 2, равна ∆ρvr. Для вентиля должно быть выполнено условие
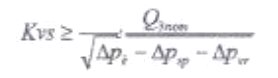
При практическом расчете выберем ближайший Kvs коэффициент из предложенного ряда данного типа вентиля.
- значение коэффициентов KvA и KvB – зависимы от хода h вентиля A, как уже было замечено при замене трехходового вентиля двумя двухходовым. Расчет действителен для любой характеристики в обеих ветвях, только при конкретном числовом вычислении следует поставить в формулы правильную функцию, соответствующей выбранной характеристике.
При расчете требуется Kv коэффициенты отдельных ветвей, которые найдем из нормальных параметров цепи, следовательно, из значений расхода Q3nom и перепадов давлений ∆ρsp и ∆ρvr, которые возникнут именно при таком расходе. Значит

Введем правильный Kv коэффициент обратной ветви B KvBred , где последовательно включены коэффициент обратной ветви Kvvr и коэффициент KvB регулирующего вентиля B. Для такого включения действительно: 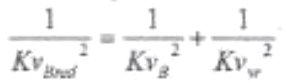
Предположим, что при открытии ветви будет давление p2 выше, чем давление p4, следовательно, не произойдет поворот течения в обратной ветви. В связи с этим для отдельных расходов действительно Q3 = Q1 + Q2 и на основании соотношения
![]()
получаем
Q3 = Q1 + Q2
Q12 = Kν12 · (p1 - p4)
Q22 = Kν2red2 · (p2 - p4)
Q32 = Kνsp2 · (p3 - p2)
Из схемы вытекают следующие соотношения:
∆ pė = p3 - p4
∆ pč = p1 - p2
p2 = konst
Разумеется, что в данный момент математической модели не зависит вычисление расхода от величины статического давления в системе (здесь предполагается ограничение расхода из-за влияния кавитации). Поэтому упростим систему управления при условии, что p2=0.
Таким образом мы получили систему семи уравнений с семью неизвестными Q1, Q2, Q3, p1, p2, p3, и p4, которая описывает нам течение через систему от начало хода вентиля до точки перехода, при условии, что Q2=0, следовательно Q1= Q3, p4= p2=0. Из вышеприведенных уравнений видно, что точка перехода наступает при ходе h вентиля А, для которого действительно:
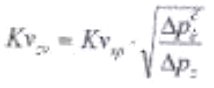
Если выбранный Kvs коэффициент трехходового регулирующего вентиля больше, чем значение Kvzv соответствующее точке перехода, то произойдет, при открывании вентиля выше значения хода h, принадлежащего Kv коэффициенту точки перехода Kvzv поворот течения в ветви В. Математическую модель, описывающую поведение системы следует преобразовать:
Q3 = Q1 - Q2
Q12 = KνA2 · (p1 - p4)
Q22 = KνBred2 · (p4 - p2)
Q3č2 = Kνsp2 · (p3 - p2)
∆ pė = p3 - p4
∆ p= = p1 - p2
p2 = konst
Эти семь уравнений описывают поведение системы от значения хода вентиля большего, чем значение, соответствующего Kv коэффициенту точки перехода Kvzv (в соответствии с выбранным значением Kvs и расходной характеристикой ветви А вентиля), до полного открытия.
Приведенные управления можно решить при помощи подобранного числового метода, поскольку точнее решение этой системы очень сложное. Вычислительная программа Вентили 2004, созданной фирмой LDM, решает семь основных типов включения двух и трехходовых вентилей в смесительной или распределительной функции. На следующих рисунках продемонстрировано ее применение для вышерешенного примера. Поступаем в таком порядке:
В программе Вентили 2004 открываем закладку с надписью: Контроль расхода через трехходовой вентиль.
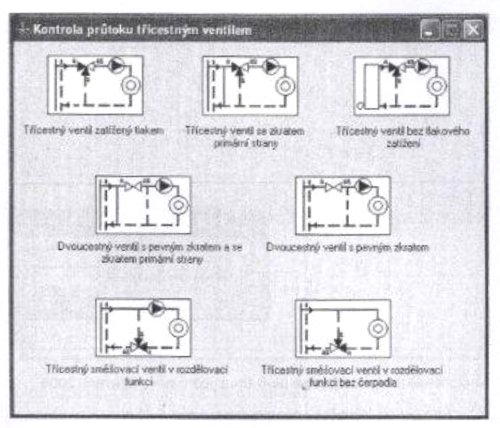
Рис. 2.12. Окно «Контроль расхода через трехходовой вентиль».
Решенному примеру соответствует верхняя схема слева. После того, как окно откроется, появится следующее окно с предварительно определенными значениями, которые можно изменить в зависимости от конкретного случая. Если оставим первоначальное значения, то увидим, что следует определить размеры и проконтролировать смесительный вентиль, чтобы по цепи потребителя протекало номинальное количество (подача) 3 м3.ч-1 при давлении насоса 0,6 бар. При таком расходе у нас уже вычислено сопротивление ветви потребителя 0,4 бар, в обратной ветви 0,05 бар. Цепь нагружена перепадом давления между подачей и обратным течением 0,4 бар. Предполагаем применение смесительного вентиля с линейной характеристикой в обеих ветвях.
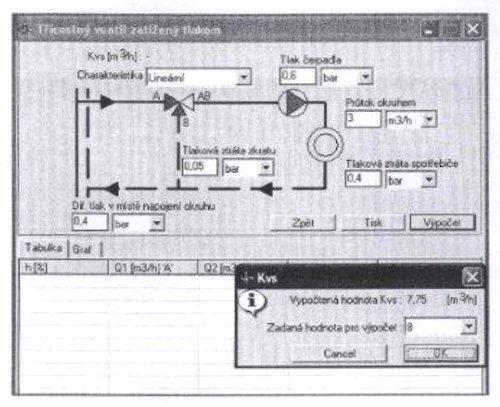
Рис. 2.13. Вычисление Kv трехходового вентиля в программе Вентили 2004.
Выполнив щелчок по кнопке Výpočet в соответствии с рис. 2.13 появится новое окно, информирующее о вычисленном значении Kv=7, 75m3.h-1 и предлагающее сделать выбор коэффициента Kvs. Из предложенных значений выбираем значение 10. В нижней части окна увидим вычисленные значение расхода Q1, Q2 и Q3 при отдельных процента хода. Жирно-напечатанный ряд информирует о достижении точки перехода при 57,31% хода (см. рис. 2.14).
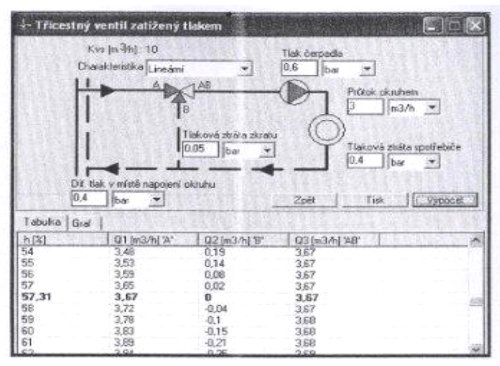
Рис. 2.14. Точка перехода для приведенного примера.
Открываем закладку Graf появится географическое изображение расхода через систему, причем значение 100% соответствует не выбранное номинальное значение 3 м3.ч-1, а действительное достигнутое максимальное значение расхода через ветви, т.е. в данном случае Q1макс=4,56 м3.ч-1.
Можем так же убедиться, что значение расхода ветви потребителя нигде не падает ниже требующегося значение Q3 ном.
С таким программным обеспечением можно осуществлять детальный анализ для различных видов и типов арматуры в каждом конкретном случае. Проводя последовательную проверку возможных рабочих состояний, можно обнаружить еще в процессе разработки проектной документации проблемы, которые могли бы возникнуть во время эксплуатации.
Например, можем сравнить уместность отдельной расходных характеристик для данного случая. На рис. 2.15, 2.16 и 2.17 видим постепенное графическое изображение расхода через описанную систему при линейной, равнопроцентной и LDMspline характеристиках в ветви А. Очевидно, что равнопроцентная и LDMspline характеристики для данного случая подходят больше, т.к. позже достигается точка перехода и для регулирования имеется в распоряжении больший диапазоне хода. Кроме того, у LDMspline характеристики в отличие от равнопроцентной не возникает характерное понижение расхода через потребитель в начале хода, расход поддерживается на почти идеальном постоянном значение , что улучшает регулирование подачи тепла в переходной период.
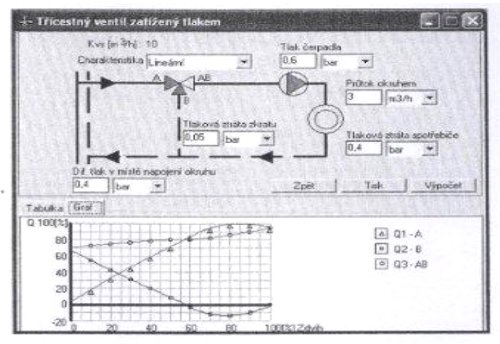
Рис. 2.15. Процесс смешения при линейной характеристике.
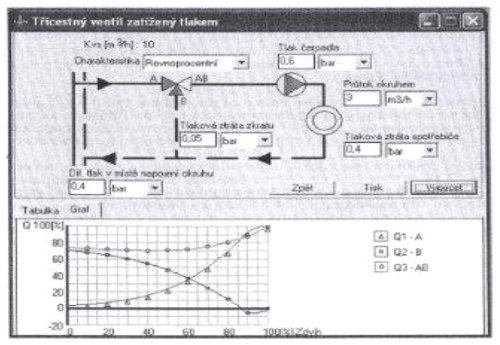
Рис. 2.16. Процесс смешения при равнопроцентной характеристике.
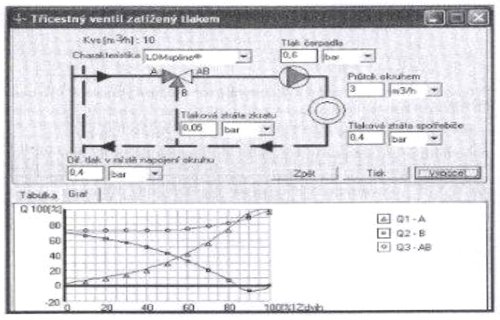
Рис. 2.16. Процесс смешения при характеристике LDMspline.